1) Basics:

Exact and Approximate Results

With no decimal point in an expression,  Mathematica gives you an exact result.

In[1]:=

2^1000

Out[1]=

1071508607186267320948425049060001810561404811705533607443750388370351051124936122493198378815 ... 53046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376

On the other hand, if you put an decimal point in an expression, then Mathematica gives  an approximate numerical result.

In[2]:=

RowBox[{2, ^, 1000.}]

Out[2]=

1.07151*10^301

π to many decimal places

In[3]:=

N[Pi, 1000]

Out[3]=

3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534 ... 98253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420199

There are thousands of mathematical functions

The arguments of a function are contained within square brackets. Functions can be nested. (You can use I or i to represent (-1)^(1/2))

In[4]:=

Cos[ArcSin[I x]]

Out[4]=

(1 + x^2)^(1/2)

Inverse[] works on both symbolic and numerical matrices. There are many other linear algebra functions.

In[5]:=

Inverse[(1 2)] 3 4

Out[5]=

{{-2, 1}, {3/2, -1/2}}

There is a function for just about anything you can think of...

In[6]:=

Series[Sin[x/(x - 2)], {x, 0, 10}]

Out[6]=

-x/2 - x^2/4 - (5 x^3)/48 - x^4/32 - x^5/3840 + (5 x^6)/512 + (6931 x^7)/645120 + (1591 x^8)/184320 + (224179 x^9)/37158912 + (31987 x^10)/8257536 + O[x]^11

In[7]:=

SphericalHarmonicY[3, 2, θ, ϕ]

Out[7]=

1/4 ^(2  ϕ) 105/(2 π)^(1/2) Cos[θ] Sin[θ]^2

Sequences of Operations

If an expression ends in ";", then its result is not displayed.  This often necessary in order suppress lengthy output.

In[8]:=

integrand = Normal[Series[Sin[x/(x - 2)], {x, 0, 100}]] ; ∫_0^1integrandx

Out[9]=

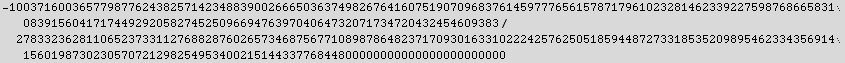
-100371600365779877624382571423488390026665036374982676416075190709683761459777656157871796102 ... 87273318535209895462334356914156019873023057072129825495340021514433776844800000000000000000000000

The List is the most basic data structure

Lists are very general objects that represent collections of expressions. Lists are used to represent sets, vectors, matrices, tensors. Lists are given in curly brackets and their elements are separated by commas. They are analogous to arrays in other computer languages, but much more powerful.

List of numbers

In[10]:=

{2, 3, 5, 7, 11, 13, 17}

Out[10]=

{2, 3, 5, 7, 11, 13, 17}

List of symbols

In[11]:=

{α, β, ψ, δ, ϵ}

Out[11]=

{α, β, ψ, δ, ϵ}

List of Lists

Note that the lists within a list do not have to be the same length.

In[12]:=

{{2, 3, 5, 7, 11, 13, 17}, {α, β, ψ, δ, ϵ}}

Out[12]=

{{2, 3, 5, 7, 11, 13, 17}, {α, β, ψ, δ, ϵ}}

Table[] is the function for making Lists

In[13]:=

Table[Prime[i], {i, 1, 10, 1}]

Out[13]=

{2, 3, 5, 7, 11, 13, 17, 19, 23, 29}

Table[] can be nested to make Lists of Lists

In[14]:=

lst = Table[Table[j/i, {j, 10}], {i, 10}]

Out[14]=

{{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {1/2, 1, 3/2, 2, 5/2, 3, 7/2, 4, 9/2, 5}, {1/3, 2/3, 1, 4/3, ... 2/9, 1/3, 4/9, 5/9, 2/3, 7/9, 8/9, 1, 10/9}, {1/10, 1/5, 3/10, 2/5, 1/2, 3/5, 7/10, 4/5, 9/10, 1}}

Getting a piece of a List

In[15]:=

lst[[2]]

Out[15]=

{1/2, 1, 3/2, 2, 5/2, 3, 7/2, 4, 9/2, 5}

In[16]:=

lst[[2, 2]]

Out[16]=

1

Length[] is very useful for determining the size of a list

Length[expr] gives the number of elements in expr.

In[17]:=

lst1 = Table[Prime[i] + 1, {i, 1000}] ; lst2 = Table[Prime[i] - 1, {i, 1000}] ; lst3 = lst1⋂lst2<br /> Length[lst3]

Out[19]=

{4, 6, 12, 18, 30, 42, 60, 72, 102, 108, 138, 150, 180, 192, 198, 228, 240, 270, 282, 312, 348 ... 2, 6828, 6870, 6948, 6960, 7128, 7212, 7308, 7332, 7350, 7458, 7488, 7548, 7560, 7590, 7758, 7878}

Out[20]=

174

Killing Mathematica

Mathematica will attempt to perform a calculation that might take several human lifetimes to complete, and sometimes it simply goes crazy.  You will probably have to kill the kernel.  Click at Kernel -> Quit Kernel -> Local

[Graphics:../HTMLFiles/index_35.gif]

Created by Mathematica  (June 17, 2004)